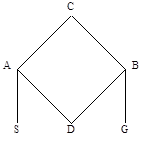Se reflejarán problemas
solucionados de la XXIX Olimpiada Matemática Española. Se debe tratar de
encontrar una solución en al menos un tiempo prudencial tras lo cual y si no lo
logramos podemos acudir a la solución o si lo logramos también, comprobando si
existen caminos alternativos de solución o hemos encontrado el mismo camino
dado. En todo caso no debe ser una búsqueda obsesiva sino más bien de
aprendizaje por lo que no es conveniente detenerse indefinidamente en un mismo
problema.
Cada competición
consta de seis problemas a solucionar, al igual que las Olimpiadas
Internaciones de Matemáticas (IMO) para las que las nacionales sirven de
preparación.

“En una reunión hay 201
personas de 5 nacionalidades diferentes. Se sabe que, en cada grupo de 6, al
menos dos tienen la misma edad. Demostrar que hay al menos 5 personas del mismo
país, de la misma edad y del mismo sexo”

“Escrito el triángulo
aritmético:
|
0 |
1 |
2 |
3 |
4 |
............. |
1991 |
1992 |
1993 |
||||||||||||||
|
1 |
3 |
5 |
7 |
............................ |
3983 |
3985 |
|
||||||||||||||
|
4 |
8 |
12 |
........................................ |
7968 |
|
||||||||||||||||
.........................................................................
donde cada número es la
suma de los dos que tiene encima (cada fila tiene un número menos y en la
última sólo hay un número). Razonar que el último número es múltiplo de 1993”

“Justificar
razonadamente que, en cualquier triángulo, el diámetro de la circunferencia
inscrita no es mayor que el radio de la circunferencia circunscrita”

“Demostrar que para
todo número primo p distinto de 2 y de 5, existen infinitos múltiplos de p de
la forma 1111......1 (escrito sólo con unos)”

“Se dan 16 puntos formando una
cuadrícula como en la figura:

De ellos se han destacado A y D. Se
pide fijar de todos los modos posibles otros dos puntos B y C con la condición
de que las seis distancias determinadas por los cuatro puntos sean distintas.
En ese conjunto de cuaternas, estudiar:
a) Cuántas figuras de 4 puntos existen
con las condiciones del enunciado.
b) Cuántas de ellas son
geométricamente distintas, es decir, no deducibles unas de otras por transformaciones
de igualdad.
c) Si cada punto se designa por un par
de enteros (Xi, Yi), razonar
que la suma:
|Xi - Xj|
+ | Yi - Yj|
extendida a los seis pares AB, AC, AD, BC, BD, CD es constante”

“Una máquina de juego de un casino tiene
una pantalla en la que se ofrece un esquema como el de la figura. Para comenzar
el juego aparece una bola en el punto S. A cada impulso que recibe del jugador,
esa bola se mueve hasta una de las letras inmediatas con la misma probabilidad
para cada una de ellas. La partida termina al ocurrir el primero de los dos
hechos siguientes:
a) La bola vuelve a S y entonces el
jugador pierde.
b) La bola llega a G y entonces el
jugador gana.
Se pide la probabilidad de que el
jugador gane y la duración media de las partidas”
|
|
Si
en cada grupo de 6 personas, 2 son de la misma edad, sólo puede haber 5 edades
diferentes, ya que, si hubiese 6 edades diferentes, eligiendo una persona de
cada edad tendríamos 6 personas de edades distintas contra la hipótesis.
Como
200 = 2 · 100 + 1Þ
al menos hay 101 personas del mismo sexo.
101 = 5 · 20 + 1 Þ
al menos hay 21 personas de la misma edad y sexo.
21 = 4 · 5 + 1 Þ al menos hay 5 personas de la
misma nacionalidad, edad y sexo.
Si representamos los elementos de la
primera fila por a0, a1, a2, ........
los elementos de la segunda
serán: a0 + a1, a1
+ a2, a2 + a3,
..............
los de la tercera serán : a0
+ 2a1 + a1, a1 + 2a2 + a3,
..............
para la cuarta : a0 + 3a1
+ 3a1 + a1, a1
+ 3a2 + 3a3 + a4,............
Supongamos que los dos primeros
elementos bp,0 y bp,1 de la fila p-ésima
son:
![]() ;
; ![]()
entonces, el primer elemento de la
fila siguiente será :
![]() (*)
(*)
en nuestro caso la primera fila tiene
1994 elementos, la segunda 1993, ... y la última corresponde a p + 1 = 1994 y
su único elemento será
![]()
Al ser 1993 primo, ![]() es múltiplo de 1993 para todo k menor que 1993
y por tanto b1993 es múltiplo de 1993.
es múltiplo de 1993 para todo k menor que 1993
y por tanto b1993 es múltiplo de 1993.
La
desigualdad propuesta, R - 2r ³ 0
es una consecuencia del teorema de Euler. “Si I, O son el incentro y el circuncentro de un triángulo, r y R los radios de las
circunferencias inscrita y circunscritas, se verifica: IO2 = R2
- 2Rr”.
Entonces
IO2 = R (R - 2r) ³ 0 Þ R - 2r ³
0.
Veamos
primero que p tiene infinitos múltiplos de la forma 999...9. Consideremos la
sucesión: 9, 99, 999, ......,999...9 (el último tiene n nueves). Entonces se
tiene:
9
= 10 - 1; 99 = 102 - 1; 999 =
103 - 1;.......999..9 = 10n - 1
en
la sucesión hay infinitos términos de la forma 10p-1 - 1 con p ¹
2, p ¹
5 y p primo.
Puesto
que, por el teorema de Fermat: 10p-1 - 1 º
1 (mód p) si p ¹ 2, p ¹
5 la afirmación queda demostrada.
Finalmente
999...9 = 9 · 111...1 entonces si p es primo con 9 (p ¹
3), p divide al producto, es primo con 9 luego divide a 111...1.
Queda
el caso p = 3 que es evidente ya que los
infinitos números: 111; 111111,
.......... son múltiplos de tres.
El
problema admite dos ejes de simetría coincidentes con las diagonales del cuadrado.
Clasificaremos las soluciones posibles por la posición del punto B respecto del
vértice A. Usaremos coordenadas enteras con origen en A.
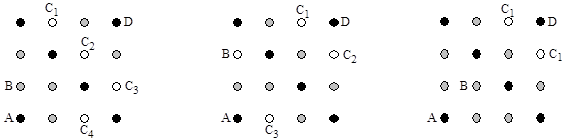
Las
tres posiciones “fundamentales” (no deducibles unas de otras por las simetrías
anteriores) son aquellas en las que B está en los puntos de coordenadas (0,1);
(0,2) y (1,1) para cada una de ellas dibujamos un esquema con las posibles
posiciones del punto C.
Las
posiciones “prohibidas” se dibujan en negro, la posición de B en gris y las de
Ci en blanco.
|
|
Un
criterio general para prohibir ubicaciones es localizar aquellos puntos que están
en la “mediatriz” de dos puntos ya situados. Como A y D son dados y fijos, la
diagonal principal siempre contiene puntos “prohibidos”
El
esquema de la izquierda contiene 4 posiciones “originales” y cada una de ellas
genera otras cuatro por aplicación de las dos simetrías, en total 16.
El
esquema del centro contiene 3 posiciones “originales” y cada una de ellas
genera otras cuatro por aplicación de las dos simetrías, en total 12.
El
esquema de la derecha contiene 1 posición “original” que genera otras cuatro
por aplicación de las dos simetrías, en total 4.
Por
tanto existen 32 posiciones posibles y 8 “originales”, esto contesta a los
apartados a) y b).
Para
el apartado c) hay que suponer que los enteros asignados a cada punto son sus
coordenadas en un origen cualquiera, nosotros supondremos que el origen está en
A con lo que las coordenadas de A son (0,0) y las de D(3,0).
los
seis sumandos corresponden a las parejas AB, AC, AD, BC, BD y CD.
El
correspondiente a AD es constante y vale 3+3 = 6.
Los
correspondientes a AB y BD valen en conjunto siempre 6 ya que A está en fila
inferior y columna izquierda y D en la fila superior y columna derecha.
Por
el mismo motivo los sumandos correspondientes a AC y CD valen entre los dos
siempre 6.
Sólo
queda el sumando |Xi - Xj| + | Yi - Yj|
correspondiente a BC que por simple comprobación en todos los casos
“originales” vale siempre 3.
La
suma completa es entonces constante y vale 6 + 6 + 6 + 3 = 21.
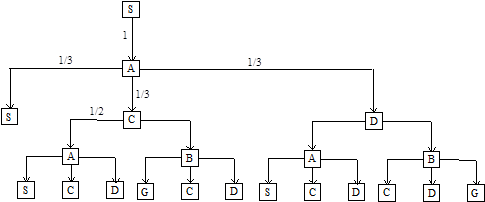
Podemos
representar el desarrollo del juego mediante un diagrama en árbol:
|
|
La
probabilidad de que el juego tenga longitud 2 es ![]()
La
probabilidad de que el juego tenga longitud 4 es :![]()
La
probabilidad de que el juego tenga longitud 6 es :![]() ,
etc., en general
,
etc., en general
la
probabilidad de que el juego tenga longitud 2n es: ![]()
Entonces,
la duración media M de un juego es la suma de cada longitud por la probabilidad
respectiva :
![]()
serie
aritmético-geométrica que se suma por el mismo método que la geométrica:
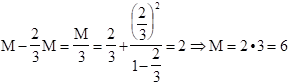
La
probabilidad P de ganar será la suma de las probabilidades de ganar en 4 pasos
más la de que gane en 6 pasos ...etc.:
![]()
joseluis.gonzalez@realidad-simulada.es
Todos los
derechos reservados son propiedad legal e intelectual exclusiva y registrada a nombre de
José Luis
González Sanz
realidad-simulada.es